(New tips are continually added to these pages.  Check back in a few months' time for more)

TOPIC 9:     Current Electricity and D.C. Circuits

Tip 1:

Most students have no problem with Kirchhoff's First Law (Current Law): "current in" equals "current out".  They have a little more problem with Kirchhoff's Second Law (Voltage Law).

Bascially, this law states that the sum total of electromotive force (e.m.f) around a loop is equal to the sum total of potential drops (p.d).  In equation form, the law is:

Se.m.f = S p.d

First, you assume a direction for the current in each branch of the circuit.  Next, you add in the "+" and "-" signs for all the e.m.f and resistors in the circuit, based on your assumed direction for the current.  Then you take "a walk" around the circuit loop (whether clockwise or anticlockwise its up to you, but you must be consistent).

The first round, you "collect" all the e.m.f (like collecting flowers).  Any e.m.f that rises along the direction of your "walk" will be assigned a positive value, and vice versa.  Put all these on the left hand side of the equation.

In the second round, you "collect" all the p.d (like collecting leaves).  Any p.d that drops along the direction of your "walk" will be assigned a positive value, and vice versa.   Put all these on the right hand side of the equation.

Finally, solve the equation.

Illustration: let's analyse the left loop of the circuit below:

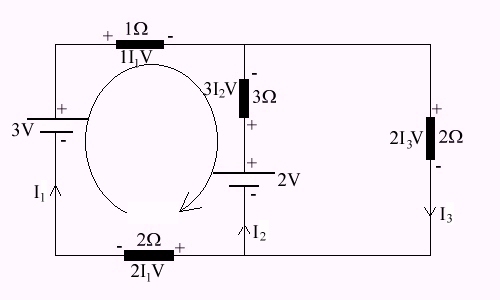
Taking clockwise as positive, let's walk around the garden picking up flowers (e.m.f)

Since the 3 V e.m.f rises along my direction of travel, I give it a positive sign; since the 2 V e.m.f drops along my direction of travel, I give it a negative sign.  Hence the left hand side of Kirchhoff's voltage equation is +3 - 2

Next, let's walk around the garden picking up leaves (p.d).

Since the 2I₁V and 1I₁V drop along my direction of travel, I give them positive signs; since the 3I₂ V rises along my direction of travel, I give it a negative sign.

Hence the equation becomes:

+3 V - 2 V = +2I₁ V + 1I₁ V - 3 I₂ V

Another equation can be obtained from the right loop.  Combining these 2 equations with the Current Law: I₁ + I₂ = I₃, all the currents and voltages can be solved (3 equations; 3 unknowns).

Tip 2:

One of the most common mistakes students make when analysing electrical circuits is to think that "potential" or "voltage" flows around the circuit.

"Potential" does not flow; it is "Current" that flows.

Let's use an analogy: Electrical Potential is like Gravitational Potential; and Electrical Current is like Water Current.

We see that water current flows from a higher potential ground (eg. top of the waterfall) to a lower potential ground (eg. bottom of the waterfall).

Similarly, electrical current flows from a point of higher potential (eg. 6 V) to a point of lower potential (eg. -8 V).

© Copyright Physics.com.sg (Registration No. 52890077C).  All rights reserved.
® First Class in Physics Tuition is the Registered Trademark (TM No. T02/02149B) of Physics.com.sg
.